Los números binarios forman parte del sistema binario, un sistema de numeración utilizado generalmente en informática en el cual los números se representan solamente mediante las cifras cero y uno (0 y 1). Al igual que sucede con los números decimales, podemos colocar números tanto a la izquierda como a la derecha del punto o la coma decimal para indicar valores mayores o menores que uno.
Un dígito binario por sí solo (como «101» ó «1001») se llama un «bit» en lenguaje informático, palabra que viene del inglés «binary digit». Por ejemplo, 11010 tiene cinco bits de longitud.
Numero Octal
El Sistema Octal, es un sistema de numeración que utiliza los dígitos del 0 al 7 para expresar sus cantidades; este sistema es muy utilizado en computación ya que es muy fácil convertir un número binario en octal y viceversa. Como una cifra expresada en el sistema binario utiliza muchos dígitos se utiliza el sistema octal para representarlos, ya que de esta forma se usan menos dígitos lo que es más comprensible para el ser humano.

Numeros Hexadecimales
Es un sistema de numeración posicional de base 16 que utiliza 16 símbolos. Recuerda que en binario había dos: el 0 y el 1. Estos 16 símbolos son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Siendo A=10, B=11, C=12, D=13, E=14 y F=15.
El sistema hexadecimal se usa mucho en informática porque dos dígitos hexadecimales corresponden a 1 byte.
Paso de hexadecimal a binario: se sustituye cada dígito hexadecimal por su valor en binario usando 4 bits. Ejemplo: B10h = 101100010000b
Paso de binario a hexadecimal: se hacen grupos de 4 bits y se sustituyen por su valor en hexadecimal. Ejemplo: 110000100101b = 1100 0010 0101 = C25h
Paso de hexadecimal a decimal: AB5h = 5×160 + 11×161 + 12×162= 2741d
Paso de decimal a hexadecimal: 269d = 10Dh
Ejercicios:

Pasa de hexadecimal a binario: CF1D4h , AF2h
Pasa de binario a hexadecimal: 00110100110b, 1010111b
Pasa de hexadecimal a decimal: 71CEh, B418Ah
Pasa de decimal a hexadecimal: 547d, 198d
Operaciones matemáticas en sistemas numéricos
Suma Binaria
Suma Binaria. La suma o adición binaria es análoga a la de los números decimales. La diferencia radica en que en los números binarios se produce un acarreo (carry) cuando la suma excede de uno mientras en decimal se produce un acarreo cuando la suma excede de nueve(9).

Resta binaria
Resta en el sistema binario. En el sistema decimal, cuando se restan dos números y el minuendo de una determinada posición del número es más chico que el sustraendo de esa misma posición, le pide un dígito al minuendo de la próxima columna de dígitos más significativos (a la izquierda). Lo mismo vale en binario
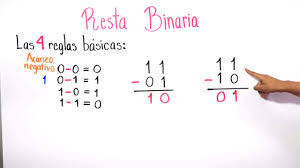
Representacion Negativa en Binarios
Otro enfoque sería representar números negativos usando el complemento a la base menos uno. En el caso de los números binarios, sería el complemento a uno y la forma del complemento a uno de un número binario es un NOT bit a bit aplicado al número, es decir, la inversión de unos por ceros y ceros por unos.

Suma de octales:
- Se empieza a sumar de derecha a izquierda.
- Sumar el/los dígitos que se encuentran en la primer columna y se coloca el resultado debajo de la columna.
- En caso de que la suma exceda la base del sistema, se restan 8, y se coloca un acarreo en la siguiente columna, el valor del acarreo depende de las veces que haya superado la base del sistema y el valor que se obtiene de la resta se coloca debajo de la columna.

Resta de octales:
Se realiza de la misma forma que en el sistema decimal, la única diferencia es que cuando se “piden cifras” al número que está al lado, pasa a la columna de la derecha como 8, luego se suma ese 8 con el numero que “pidió” la cifra y se continua con la operación.
Cuando el segundo número (sustraendo) es mayor que el primero (minuendo) el resultado (diferencia) será negativo.

Suma hexadecimal
Cumple los mismos requisitos que la suma octal, la única diferencia es la base del sistema que se resta.
- Se empieza a sumar de derecha a izquierda.
- Sumar dígitos que se encuentran en la primer columna y se coloca el resultado debajo de la columna.
- En caso de que la suma exceda la base del sistema, se escribe el resultado y se le restan 16, se coloca un acarreo en la siguiente columna, el valor del acarreo depende de las veces que haya superado la base del sistema y el valor que se obtiene de la resta se coloca debajo de la columna.

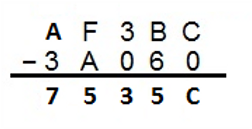
Resta hexadecimal
Se realiza de la misma forma que en el sistema decimal, la única diferencia es que cuando se “piden cifras” al número que está al lado, pasa a la columna de la derecha como 16, luego se suma ese 16 con el numero que “pidió” la cifra y se continua con la operación.
Bitwise Operators
Los operadores bitwise son similares a los operadores lógicos, excepto que funcionan en una escala más pequeña: representaciones binarias de datos.
Los siguientes operadores están disponibles:
op1 & op2 – El operador AND compara dos bits y genera un resultado de 1 si ambos bits son 1; De lo contrario, devuelve 0.
op1 | op2 – El operador OR compara dos bits y genera un resultado de 1 si los bits son complementarios; De lo contrario, devuelve 0.
op1 ^ op2 : el operador OR EXCLUSIVO compara dos bits y devuelve 1 si cualquiera de los bits es 1 y da 0 si ambos bits son 0 o 1.
~ op1 – El operador COMPLEMENTO se usa para invertir todos los bits del operando.
op1 >> op2 – El operador SHIFT RIGHT mueve los bits a la derecha, descarta el bit del extremo derecho y asigna un valor de 0 al bit de la izquierda. Cada movimiento a la derecha divide efectivamente op1 en la mitad.
op1 << op2 : el operador MAYÚS IZQUIERDA mueve los bits a la izquierda, descarta el bit del extremo izquierdo y asigna un valor de 0 al bit de la derecha. Cada movimiento a la izquierda multiplica efectivamente op1 por 2.
Los operadores bitwise se utilizan para cambiar bits individuales en un operando. Un solo byte de la memoria de la computadora, cuando se ve como 8 bits, puede significar el estado verdadero / falso de 8 indicadores porque cada bit se puede usar como una variable booleana que puede contener uno de dos valores: verdadero o falso. Una variable de marca se usa normalmente para indicar el estado de algo. Por ejemplo, los archivos de computadora se pueden marcar como de solo lectura. Por lo tanto, es posible que tenga una variable $ fReadOnly cuyo trabajo sería mantener el estado de solo lectura de un archivo. Esta variable se llama variable de bandera porque cuando $ fReadOnly tiene un valor verdadero, es equivalente a un árbitro de fútbol que lanza una bandera. La variable dice: «Whoa! No modifique este archivo».
Cuando tiene más de una variable de bandera, puede ser más eficiente usar una sola variable para indicar el valor de más de una bandera. El siguiente ejemplo te muestra cómo hacer esto.








